
Let $\]^2$ which is the biased variance estimator. and to propose various estimation techniques (method of moments, mixed moments, maximum likelihood etc.). with E(X) 1/ E ( X) 1 / and E(X2) 2/2 E ( X 2) 2 / 2. Like for the Burr distribution, the maximum likelihood and method of moments estimators can only be evaluated numerically. Suppose you have to calculate the GMM Estimator for of a random variable with an exponential distribution. equation (equivalent to identication when only () is imposed), a method-of-moments estimator is dened as a solution (or near-solution) of a sample analogue to (), replacing the population expectation by a sample average.

Thus, the probability that all n sample values are greater than x is. Method of moments estimators (MMEs) are found by equating the sample moments to the corresponding population moments. It seems reasonable that this method would provide good estimates, since the empirical. Higher moments of a random variable Binomial, Poisson, Normal and Exponential distributions Joint distribution. Here is the definition of method of moments estimation in my book: GMM Estimator of an Exponential Distribution. Method of Moments (MOM) By definition (1.5), the kth moment of the Pareto distribution is given as: In order to obtain the estimate of from a sample of n observations, we recall that the probability of an observation greater than x is. The method of moments, introduced by Karl Pearson in 1894, is one of the oldest methods of estimation. The resulting values are called method of moments estimators. My understanding of method of moments estimation is bad.
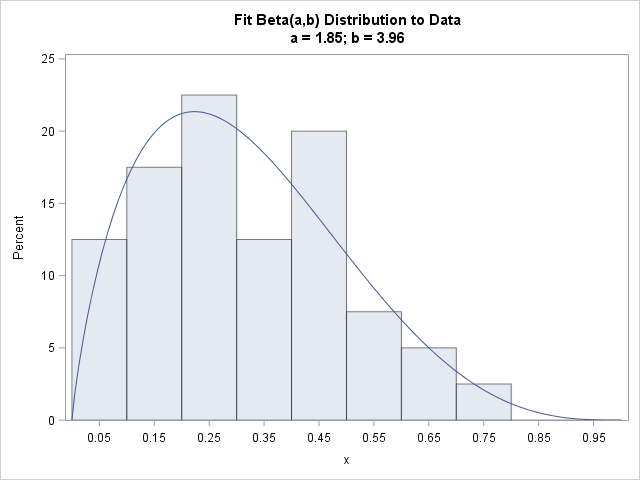
For data X 1, X 2,, X n from a normal population the method of moments estimator (MME) of the population mean is the sample mean X and the population variance S 2 is the MME.
#METHOD OF MOMENTS ESTIMATOR FOR EXPONENTIAL DISTRIBUTION HOW TO#
Let $K_1 \ldots K_n$ (in your case: $\pmb$ is the inverse of the sample mean of data.I am sorry in advance if this question seems like low effort, but I really do not know how to solve this problem. You cannot use the classical 'method of moments' method to estimate parameters of a distribution without knowing the distribution and its parameters.


 0 kommentar(er)
0 kommentar(er)
